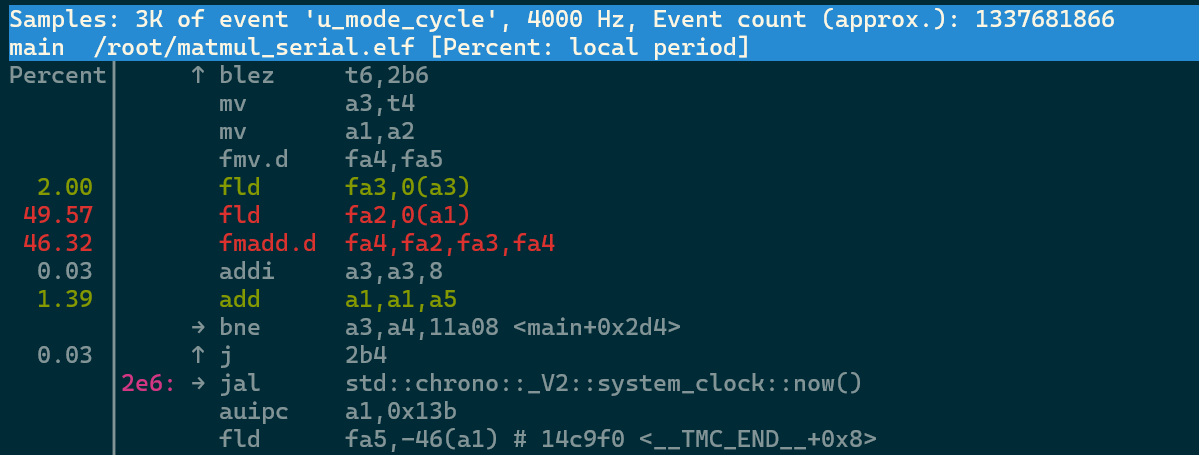
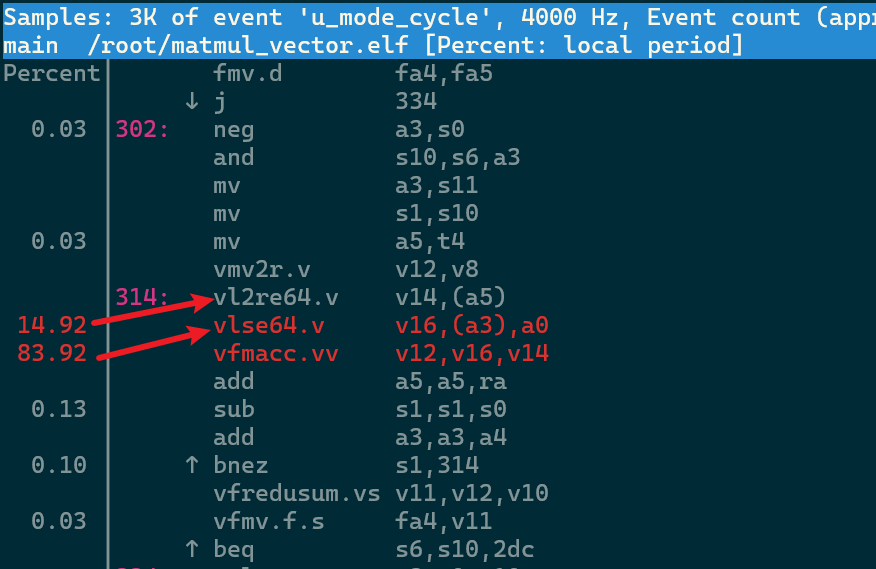
Hi,
I tried to use the passes mentioned here to enable auto-vectorizaton for RVV. In order to compare with serial one, I compile it with and without auto-vec passes. But they have almost the same execution time on Spacemit(R) X60!
My code is:
#include <iostream>
#include <fstream>
#include <cstdlib>
#include <cmath>
#include <cassert>
#include <chrono>
using namespace std;
using std::chrono::high_resolution_clock;
using std::chrono::milliseconds;
typedef double data_t;
int read_matrix_dimensions(FILE *file, size_t *M, size_t *K, size_t *N);
void read_vector(FILE *file, double *vector, size_t size, size_t rowSize);
extern bool compare(size_t dm, size_t dn, data_t *a, data_t *b);
extern void matmul(data_t *a, data_t *b, data_t *c, int n, int m, int p);
void matmul(data_t *a, data_t *b, data_t *c, int n, int m, int p) {
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
c[i * n + j] = 0;
#pragma omp simd
for (int k = 0; k < p; ++k) {
c[i * n + j] += a[i * p + k] * b[k * n + j];
}
}
}
}
bool compare(size_t dm, size_t dn, data_t *a, data_t *b) {
bool mismatch = false;
for (size_t i = 0; i < dm; i++) {
for (size_t j = 0; j < dn; j++) {
if (std::abs(a[i*dn+j] - b[i*dn+j]) > 1e-10) {
mismatch = true;
cout << "Mismatch at [" << i << "][" << j << "]: "
<< a[i*dn+j] << " != " << b[i*dn+j] << endl;
}
}
}
return mismatch;
}
int main(int argc, char **argv) {
if (argc != 2) {
cout << "Usage:\n\t" << argv[0] << " <inputFile>\n";
exit(1);
}
// Read input data from file
char *inputFile = argv[1];
FILE *file = fopen(inputFile, "r");
if(file == NULL) {
cerr << "ERROR: Unable to open file '" << inputFile << "'\n";
exit(1);
}
size_t M, K, N;
char line[16];
if (read_matrix_dimensions(file, &M, &K, &N)) {
cerr << "Error reading the matrix dimensions.\n";
} else {
cout << "Matrix Dimensions: M " << M << ", K " << K << ", N " << N << endl;
}
data_t *M1 = new data_t[M*K];
data_t *M2 = new data_t[K*N];
data_t *result = new data_t[M*N];
data_t *reference = new data_t[M*N];
// Read Matrix A
read_vector(file, M1, M*K, K);
// Read Matrix B
fgets(line, sizeof(line), file); // Read the blank line
read_vector(file, M2, K*N, N);
// Read Matrix Reference
fgets(line, sizeof(line), file); // Read the blank line
read_vector(file, reference, M*N, N);
fclose(file);
// Time measurement using chrono
high_resolution_clock::time_point beginTime = high_resolution_clock::now();
matmul(M1, M2, result, N, M, K);
high_resolution_clock::time_point endTime = high_resolution_clock::now();
std::chrono::duration<double> time_interval = endTime - beginTime;
cout << "matrixmul time: " << time_interval.count() << " seconds" << endl;
if(compare(M, N, result, reference)) {
cout << "Verification failed!\n";
return 1;
} else {
cout << "Verification passed!\n";
}
delete[] M1;
delete[] M2;
delete[] result;
delete[] reference;
return 0;
}
void read_vector(FILE *file, double *vector, size_t size, size_t rowSize) {
double *ptr = vector;
int index = 0;
double value;
while (index < size) {
// Read ELEMENTS_PER_LINE values from each line
for (int i = 0; i < rowSize && index < size ; i++) {
if (fscanf(file, "%lf", &value) != 1) {
fprintf(stderr, "Error reading value\n");
exit(EXIT_FAILURE);
}
*(ptr + index++) = value;
}
// Handle the newline character if present
int ch = fgetc(file);
if (ch != '\n' && ch != EOF) {
ungetc(ch, file);
}
}
}
int read_matrix_dimensions(FILE *file, size_t *M, size_t *K, size_t *N) {
char line[100]; // Buffer to store the line read from the file
// Read a line from the file
if (fgets(line, sizeof(line), file) != NULL) {
// Parse the dimensions using sscanf
if (sscanf(line, "%zd %zd %zd", M, K, N) != 0) {
return 0; // Successfully read all dimensions
} else {
return 1; // Error parsing the dimensions
}
} else {
return 1; // Error reading the line
}
}
And I use the following shell to compile:
# Compile serial version
echo "Compiling serial version..."
clang++ --target=riscv64-unknown-linux-gnu \
--sysroot=${RISCV_GNU_TOOLCHAIN_DIR}/sysroot \
--gcc-toolchain=${RISCV_GNU_TOOLCHAIN_DIR} \
-march=rv64gc -mabi=lp64d \
-static -g -O2 \
-o bin/matmul_serial.elf src/main.cpp
${OBJDUMP} -d -S --source-comment="@src" bin/matmul_serial.elf > bin/matmul_serial.dump
# Compile vector version
echo "Compiling vector version..."
clang++ -O2 --target=riscv64-unknown-linux-gnu \
--sysroot=${RISCV_GNU_TOOLCHAIN_DIR}/sysroot \
--gcc-toolchain=${RISCV_GNU_TOOLCHAIN_DIR} \
-march=rv64gcv1p0 -menable-experimental-extensions -mllvm --riscv-v-vector-bits-min=256 \
-fvectorize -ffast-math \
-static -g \
-o bin/matmul_vector.elf src/main.cpp
# -march=rv64gcv_zvl256b -mabi=lp64d \
${OBJDUMP} -d -S --source-comment="@src " bin/matmul_vector.elf > bin/matmul_vector.dump
# Compile vector version with tail folding
echo "Compiling vector version with tail folding..."
clang++ -O2 --target=riscv64-unknown-linux-gnu \
--sysroot=${RISCV_GNU_TOOLCHAIN_DIR}/sysroot \
--gcc-toolchain=${RISCV_GNU_TOOLCHAIN_DIR} \
-march=rv64gcv1p0 -menable-experimental-extensions -mllvm --riscv-v-vector-bits-min=256 \
-fvectorize -ffast-math \
-mllvm -prefer-predicate-over-epilogue=predicate-else-scalar-epilogue \
-mllvm -force-tail-folding-style=data-with-evl \
-static -g \
-o bin/force-tail-folding-style_matmul_vector.elf src/main.cpp
# -march=rv64gcv_zvl256b -mabi=lp64d \
${OBJDUMP} -d -S --source-comment="@src " bin/force-tail-folding-style_matmul_vector.elf > bin/force-tail-folding-style_matmul_vector.dump
My clang version is:
# clang -v
clang version 20.0.0git (https://github.com/llvm/llvm-project.git 86b69c31642e98f8357df62c09d118ad1da4e16a)
Target: x86_64-unknown-linux-gnu
Thread model: posix
InstalledDir: /buildSrc/llvm/llvm-project/build/bin
Build config: +assertions
Found candidate GCC installation: /usr/lib/gcc/x86_64-linux-gnu/11
Selected GCC installation: /usr/lib/gcc/x86_64-linux-gnu/11
Candidate multilib: .;@m64
Candidate multilib: 32;@m32
Candidate multilib: x32;@mx32
Selected multilib: .;@m64
I found, there are some vector instructions when using auto-vec passes in the dumped code.
00000000000117fe <main>:
@src }
@src
@src int main(int argc, char **argv) {
117fe: 7151 addi sp,sp,-240
11800: f586 sd ra,232(sp)
11802: f1a2 sd s0,224(sp)
11804: eda6 sd s1,216(sp)
11806: e9ca sd s2,208(sp)
11808: e5ce sd s3,200(sp)
1180a: e1d2 sd s4,192(sp)
1180c: fd56 sd s5,184(sp)
...
@src high_resolution_clock::time_point beginTime = high_resolution_clock::now();
119a4: 313010ef jal 134b6 <_ZNSt6chrono3_V212system_clock3nowEv>
@src matmul(M1, M2, result, N, M, K);
119a8: 45c2 lw a1,16(sp)
@src high_resolution_clock::time_point beginTime = high_resolution_clock::now();
119aa: 8a2a mv s4,a0
@src for (int i = 0; i < m; ++i) {
119ac: 0eb05c63 blez a1,11aa4 <main+0x2a6>
119b0: 4281 li t0,0
119b2: 4301 li t1,0
@src matmul(M1, M2, result, N, M, K);
119b4: 4e22 lw t3,8(sp)
119b6: 4802 lw a6,0(sp)
@src for (int i = 0; i < m; ++i) {
119b8: 1586 slli a1,a1,0x21
119ba: c22024f3 csrr s1,vlenb
119be: f20007d3 fmv.d.x fa5,zero
119c2: 0d907557 vsetvli a0,zero,e64,m2,ta,ma
119c6: 5e003457 vmv.v.i v8,0
119ca: 0215d893 srli a7,a1,0x21
119ce: 0034d513 srli a0,s1,0x3
119d2: 00149093 slli ra,s1,0x1
119d6: 8089 srli s1,s1,0x2
119d8: 02081713 slli a4,a6,0x20
119dc: 020e1593 slli a1,t3,0x20
119e0: 02075b13 srli s6,a4,0x20
119e4: 0205de93 srli t4,a1,0x20
@src for (int k = 0; k < p; ++k) {
119e8: 8375 srli a4,a4,0x1d
@src for (int i = 0; i < m; ++i) {
119ea: 02ab0533 mul a0,s6,a0
119ee: 0512 slli a0,a0,0x4
119f0: 42006557 vmv.s.x v10,zero
119f4: a029 j 119fe <main+0x200>
119f6: 0305 addi t1,t1,1
119f8: 92f2 add t0,t0,t3
119fa: 0b130563 beq t1,a7,11aa4 <main+0x2a6>
@src for (int j = 0; j < n; ++j) {
119fe: ff005ce3 blez a6,119f6 <main+0x1f8>
11a02: 4d01 li s10,0
11a04: 02029593 slli a1,t0,0x20
11a08: 03630633 mul a2,t1,s6
11a0c: 0205d693 srli a3,a1,0x20
11a10: 81f5 srli a1,a1,0x1d
11a12: 060e slli a2,a2,0x3
11a14: 96f6 add a3,a3,t4
11a16: 00bc03b3 add t2,s8,a1
11a1a: 00ca8fb3 add t6,s5,a2
11a1e: 068e slli a3,a3,0x3
11a20: 96e2 add a3,a3,s8
11a22: 00bc0f33 add t5,s8,a1
11a26: 8dca mv s11,s2
11a28: a039 j 11a36 <main+0x238>
@src c[i * n + j] += a[i * p + k] * b[k * n + j];
11a2a: 00ebb027 fsd fa4,0(s7)
@src for (int j = 0; j < n; ++j) {
11a2e: 0d05 addi s10,s10,1
11a30: 0da1 addi s11,s11,8
11a32: fd6d02e3 beq s10,s6,119f6 <main+0x1f8>
@src c[i * n + j] = 0;
11a36: 003d1b93 slli s7,s10,0x3
11a3a: 9bfe add s7,s7,t6
11a3c: 000bb023 sd zero,0(s7)
@src for (int k = 0; k < p; ++k) {
11a40: ffc057e3 blez t3,11a2e <main+0x230>
11a44: 009ef663 bgeu t4,s1,11a50 <main+0x252>
11a48: 4c81 li s9,0
11a4a: 22f78753 fmv.d fa4,fa5
11a4e: a825 j 11a86 <main+0x288>
11a50: 409005b3 neg a1,s1
11a54: 00befcb3 and s9,t4,a1
11a58: 003b1413 slli s0,s6,0x3
11a5c: 866e mv a2,s11
11a5e: 85e6 mv a1,s9
11a60: 879e mv a5,t2
11a62: 9e80b657 vmv2r.v v12,v8
@src c[i * n + j] += a[i * p + k] * b[k * n + j];
11a66: 2287f707 vl2re64.v v14,(a5)
11a6a: 0a867807 vlse64.v v16,(a2),s0
11a6e: 9786 add a5,a5,ra
11a70: 8d85 sub a1,a1,s1
11a72: b2e81657 vfmacc.vv v12,v16,v14
11a76: 962a add a2,a2,a0
11a78: f5fd bnez a1,11a66 <main+0x268>
@src for (int k = 0; k < p; ++k) {
11a7a: 06c515d7 vfredusum.vs v11,v12,v10
11a7e: 42b01757 vfmv.f.s fa4,v11
11a82: fb9e84e3 beq t4,s9,11a2a <main+0x22c>
...
And I also used perf to check their statistic, I find the serial version has the pretty close stat to “vectorized” one:
$ perf stat -e cycles,instructions,branches ./matmul_vector.elf input/data_256.in
Matrix Dimensions: M 256, K 256, N 256
matrixmul time: 0.711765 seconds
Verification passed!
Performance counter stats for './matmul_vector.elf input/data_256.in':
1335916948 cycles:u
224380898 instructions:u # 0.17 insn per cycle
32588608 branches:u
0.838619409 seconds time elapsed
0.810794000 seconds user
0.028096000 seconds sys
$ perf stat -e cycles,instructions,branches ./matmul_serial.elf input/data_256.in
Matrix Dimensions: M 256, K 256, N 256
matrixmul time: 0.727293 seconds
Verification passed!
Performance counter stats for './matmul_serial.elf input/data_256.in':
1359301232 cycles:u
309911765 instructions:u # 0.23 insn per cycle
47137602 branches:u
0.853090387 seconds time elapsed
0.829352000 seconds user
0.024039000 seconds sys
$ perf stat -e cycles,instructions,branches ./force-tail-folding-style_matmul_vector.elf input/data_256.in
Matrix Dimensions: M 256, K 256, N 256
matrixmul time: 0.691399 seconds
Verification passed!
Performance counter stats for './force-tail-folding-style_matmul_vector.elf input/data_256.in':
1287932652 cycles:u
313195358 instructions:u # 0.24 insn per cycle
47137667 branches:u
0.819679082 seconds time elapsed
0.784308000 seconds user
0.024132000 seconds sys
Where am I wrong? How should I do to see the difference between serial and vectorization?
Thanks